چوارگۆشەی جادوویی

چوارگۆشەی جادوویی (بە ئینگلیزی: Magic square) بریتییە لە خشتەیەکی، $n$ * $n$ ، کە خانەکانی بە ژمارە ئەرێنییەکان لە $1$ ھەتا $n^{2}$ بە جۆرێک پڕ کراوەتەوە، کە سەرجەمی ژمارەکانی ھەر ڕیزێکی ئاسۆیی و ھەر ستوونێک یان ھەر یەک لە تیرە سەرەکییەکانی، ژمارەیەکی نەگۆڕە. زۆرتر بەم شێوە باوە کە تێیدا ژمارەکان لە $1$ تا $n^{2}$ دەنوێنرێن، بەڵام ھەندێک جار، بۆ وشەکانیش کەلکی لێ وەردەگیرێت.

ئەم ژمارە نەگۆڕە بەم شێوە دەدۆزرێتەوە و پێی دەوترێت، نەگۆڕی جادوویی یان سەرجەمی جادوویی:

${\frac {n(n^{2}+1)}{2}}.$

بۆ نموونە نەگۆڕی جادوویی کاتێک $n$ یەکسان بێت بە ٣، ٤، ٥ و ٦ دەکاتە:

١١١، ٬٦٥ ٬٣٤ ٬١٥

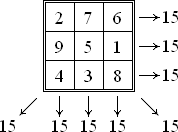
چووکەترین چوارگۆشەی جادوویی بریتییە لە چوارگۆشەیەکی ٣*٣.

کورتەمێژوو

لە درێژایی سەدەکاندا چوارگۆشەی جادوویی لەلای مرۆڤ شتێکی سەرنجڕاکێش بووە و زۆرتر لە ٤٠٠٠ ساڵە لە چاندە جیاوازەکان لەوانە ھیند و ئەورووپا، زۆرتر بەشێوەی ھەڵکۆڵراو لەسەر کانزاکان و بەردەکانەوە بینراوە. لەسەر ئەم باوەڕە بوون کە چوارگۆشەی جادوویی خاوەنی بنەمای نجومی و پێشگۆیی بووە و پێشگۆکان بۆ پێوانی تەمەن و پێشگرتن لە نەخۆشییەکان بەکاریان ھێناوە. بۆ نموونە، لە ھیندستان چوارگۆشەیەکی ٣×٣ لەسەر زەوی دەکێشنەوە بە ناوی Kubera-Kolam کە ھەمان چوارگۆشەی جادوویی لە پلەی سێیە، بەو جیاوازییەی ھەر یەک لە خانەکانی لەگەڵ ١٩ کۆ کراوەتەوە، بەشێوەیەک نەگۆڕی جادوویییەکەی دەکاتە ٧٢، چوارگۆشەکە بەم شێوەیە:

٢٣	٢٨	٢١
٢٢	٢٤	٢٦
٢٧	٢٠	٢٥

ئالبێرشت دورێر

چوارگۆشەی جادوویی ئالبێرشت

چوارگۆشەی جادوویی Albrecht Dürer لە Melencolia I ھەڵکۆڵراوە، یەکەم چوارگۆشەی جادوویییە لە ئەورووپا و لە چوارگۆشەی جادوویی Yang Hui دەچێت کە ٢٥ ساڵ پێشAlbrecht Dürer لە چین دروست کراوە، ژمارەی جادوویییەکەی دەکاتە ٣٤. لەم چوارگۆشەدا سەرەڕای ڕیز و ستوون و تیرە سەرەکییەکان، سەرجەمی چوارگۆشەی چوارینەی ناوەڕاست و چوارگۆشە چوارینەکانی چوار گۆشەکانیش دەکاتەوە ٣٤ و دوو ژمارەی ناوەڕاست لە ڕیزی چوارەمدا ڕێکەوتی ھەڵکۆڵینەکە نیشان دەدات کە یەکسانە بە ١٥١٤.

ساگرادا فامیلیا

جۆزێف سابیراچز چوارگۆشەیەکی لە پلەی ٤ لە کلێسای Sagrada Família ھەڵکۆڵیوە کە ژمارە جادوویییەکەی یەکسانە بە ٣٣. لە ڕاستیدا زۆر لە چوارگۆشەی جادوویی Albrecht Dürer دەچێت، بەو جیاوازییەی کە لە ٤دانە لە خانەکانی یەک دەرکراوە.

١	١٤	١٤	٤
١١	٧	٦	٩
٨	١٠	١٠	٥
١٣	٢	٣	١٥

ئەم چوارگۆشەیە، جیاوازە لە چوارگۆشەیەکی ئاسایی، لەبەر ئەوەی دوو ژمارەی ١٤ و ١٠ دوو جار تێیدا ھاتووە و ژمارە ١٢ و ١٦ی تێدا نییە.

لە وڵاتە جۆراوجۆرەکاندا

ئەورووپا

لە دەوروبەری ساڵی ١٣٠٠ی زایینی لەدوای وەرگێڕانی کتێبی شەمسولمەعاریف لە ئەورووپا چەندین کتێب لەبارەی چوارگۆشەی جادووییدا نووسران. مانوێل موخبولۆسی یۆنانی لە یەکەم کەسانێک بوو کە کاری لەسەر وەرگێڕانی کتێبەکەی ئەلبەنی کرد. ھەروەھا لە دەقە ئیسپانییەکاندا، ھەندێک بابەت ھەیە کە پەیوەندی بە چوارگۆشەی جادوویی ھەیە. چوارگۆشە جادوویییەکان لە ئیتالیاش لە سەدەکانی ناوەڕاستدا باو بوون، لوکا پاککویا لەسەر چوارگۆشە جادوویییەکان لە پلەی ٣ تا ٩ کاری زۆری ئە ئەنجام داوە.

ئەلگۆریتم

شیکاریی چوارگۆشە جادووییەکان بە بەکارھێنانی ئەلگۆریتمەکان زۆر ئاسان دەبێت و دەکرێت بە ھەر زمانێکی بەرنامەسازی، بەرنامەیان بۆ دروست بکرێت. بۆ نموونە، بەکارھێنانی زمانی جاڤا، دەتوانرێت فانکشنی چوارگۆشەی جادوویی بۆ ھەر ژمارەیەکی سروشتی دروست بکرێت کە بە شێوەی خوارەوەیە:^[١]

<html>
<script>
function magic(n)
{
   var i=0, j=(n-1)/2, p, k, m=[],  m1=[], m2=[];
    if(n<=0 || n-Math.ceil(n)!=0) return 'Error: n must be a positive integer..';
    if(n==2) return 'Error: there is no magic square of 2x2 !';
    if(n%4==0){//Double Even
        for (i=0; i<n/2; i++){
            for (j=0; j<n; j++){
                if((((i%4==0)||(i%4==3))&&((j%4==1)||(j%4==2)))||(((j%4==0)||(j%4==3))&&((i%4==1)||(i%4==2)))){
                    m1[j]= i*n+j+1;
                    m2[n-j-1]= n*(n-i)-j;
                }
                else{
                    m1[j]= n*(n-i)-j;
                    m2[n-j-1]=i*n+j+1;
                }            }
            m[i]=m1;
            m[n-i-1]=m2;
            m1=[];
            m2=[];
        }
    }
    else if(n%2==0){//Single Even
        p = n/2;
        m1 = magic(p);
        for (i=0; i<2*p; i++)m[i]=[];
        for (i=0; i<p; i++)for(j=0; j<p; j++){
            m[i][j] = m1[i][j]*1;
            m[i][j+p] = m1[i][j]*1+2*p*p;
            m[i+p][j] = m1[i][j]*1+3*p*p;
            m[i+p][j+p] = m1[i][j]*1+p*p;
         }
        for(i=0; i<p; i++){
            k = (n-2)/4;
            for(j=0; j<k; j++){
                k2=m[i][j];
                m[i][j]=m[i+p][j];
                m[i+p][j]=k2;
            }
        }
        for(i=0; i<p; i++){
            for(j=n-k+1; j<n; j++){
                k2=m[i][j];
                m[i][j]=m[i+p][j];
                m[i+p][j]=k2;
            }
        }
        k2=m[k][0]; m[k][0]=m[k+p][0]; m[k+p][0]=k2;
        k2=m[k][k]; m[k][k]=m[k+p][k]; m[k+p][k]=k2;
    }
    else{// Odd
        for (k=1; k<=n*n; k++)
        {
            m2[i*n +j] = k;
            i--;
            j++;
            if (k%n == 0){
                i += 2;
                j--;
            }
            if (j==n)j = 0;
            if (i==-1) i = n-1;
        }
        for(i=0;i<n;i++){for(j=0;j<n;j++)m1[j]=m2[i*n+j];m[i]=m1;m1=[];}
    }
    m[0][0]=' '+m[0][0];
    for (k=0; k<n; k ++) m[k][n-1] += '\n';
    return m;
}
</script>
<noscript> Java script must be enabled..<br /> </noscript>
<body>
Magic square of <input id=ent value="6">
<input type="button" value = " = " onclick ="disp.value=magic(ent.value*1)">
<br /><textarea id="disp" style="width: 780px; height: 300px">
</textarea>
</body>
</html>

پەراوێزەکان

^ HTML جاڤا 29 June 2012^{[Date mismatch]} لە وەیبەک مەشین ئەرشیڤ کراوە.

سەرچاوەکان

بەشداربووانی ویکیپیدیا، «مربع جادویی»، ویکیپیدیای فارسی. سەردان لە ٢٢ شوباتی ٢٠١٩.

دەروازەی ماتماتیک

ئەم «ماتماتیک» وتارە کۆلکەیەکە. دەتوانیت بە فراوانکردنی یارمەتیی ویکیپیدیا بدەیت.

[1] HTML جاڤا 29 June 2012^{[Date mismatch]} لە وەیبەک مەشین ئەرشیڤ کراوە.

[١]