پەڕگە:Mandelbrot Components.svg

پەڕگەی سەرەکی (پەڕگەی SVG، بە ناو ١٬٠٠٠ × ١٬٠٠٠ پیکسەڵ، قەبارەی پەڕگە: ٨٥٣ کیلۆبایت)
ئەم پەڕگە لە Wikimedia Commonsەوەیە و لەوانەیە لە پڕۆژەکانی دیکەش بەکار ھاتبێت. پێناسەکەی لەسەر پەڕەی وەسفی پەڕگەکە لە خوارەوە نیشان دراوە.
پێڕست
- 1 کورتە
- 2 Description with Maxima code
- 3 Maxima source code
- 4 References
- 5 Acknowledgements
کورتە
| وەسفMandelbrot Components.svg |
English: SVG version of File:Components1.jpg, created using maxima by modifying preamble line of code to the following:
user_preamble="set terminal svg size 1000,1000;set out 'mysvg.svg';set size square;set key out vert;set key bot center",[1] |
| ڕێکەوت | |
| سەرچاوە | maxima code from File:Components1.jpg |
| بەرھەمھێنەر | Gringer (talk) |
| وەشانەکانی تر |
|
Description with Maxima code
Boundaries of hyperbolic components of Mandelbrot sets are closed curves : cardioids or circles.
Douady-Hubbard-Sullivan theorem (DHS) states that unit circle can be mapped to boundary of hyperbolic component. This relation is defined by boundary equations. Here these equations are used to draw boundaries of hyperbolic components.
Douady-Hubbard-Sullivan theorem
The Douady-Hubbard-Sullivan theorem (DHS) states that the multiplier map 


Here it is important that it maps the boundary of a hyperbolic component to the boundary of the unit disk ( = unit circle ) :

and its inverse function maps the unit circle to the boundary of hyperbolic components :

The algorithm
Draft algorithm
The algorithm consist of
- rasterisation of a circle ( closed curve) parametrised by angle
- complex mapping circle points to boundary points of a hyperbolic component
Detailed algorithm
For given period 
- Decide how many points of closed curve you want to draw ( iMax ).
- Compute
- start with
- while
repeat :
- compute point of the unit circle in the standard plane
where
is an internal angle,
- map points onto the parameter plane (complex mapping ) using one of 2 methods :
- using explicit function
( it is possible only for periods 1-3)
- solving implicit equation
with respect to
( it is posible for periods 1-8 using numerical methods)
- using explicit function
- compute new angle
- compute point of the unit circle in the standard plane
- draw set of points, which looks like curve[3]
Relations between hyperbolic components and unit circle
Definitions
f(z,c):=z*z+c;
F(n, z, c) := if n=1 then f(z,c) else f(F(n-1, z, c),c);
Multiplier of periodic orbit :

_lambda(n):=diff(F(n,z,c),z,1);
Unit circle 

where coordinates of 

Boundary equations
Boundary equation
- defines relations between hyperbolic components and unit circle for given period
,
- allows computation of exact coordinates of hyperbolic componenets.

Equations are in papers of Brown[4],John Stephenson[5], Wolf Jung[6]. Methods of finding boundary equations are also described in WikiBooks.
For boundary points :

so boundary equations can be in 4 equivalent forms :
period 
|

|

|
exponential 
|
trigonometric 
|
|---|---|---|---|---|
| 1 | 
|

|

|

|
| 2 | 
|

|

|

|
For higher periods only P-form is used, because it is the shortest and usefull for computations.
for period 3 :

for period 4 :

for period 5 :

Solving boundary equations with respect to c
Boundary equations for periods:
- 1-3 it can be solved with symbolical methods and give explicit solution :
- 1-2 it is easy to solve[7]
- 3 it can be solve using "elementary algebra" ( Stephenson )
- >3 it can't be solved explicitly and must be solved numerically with respect to
.
period 1

There is only one period 1 component.[8] Because boundary equation is simple :

so it is easy to get inverse multiplier map :

For each internal angle 
- point on unit circle
,
- point
Result is a list of boundary points 
period 2
Because boundary equation is simple :

so it is easy to get inverse multiplier map :

For each internal angle 
- point on unit circle
,
- point
Result is a list of boundary points 
period 3

There are 3 period 3 components[9]
Here solution of boundary equation gives 3 inverse multiplier maps 
It is possible in 3 ways :
- Munafo method[10] (every functions maps one half of one component and one half of other component)
- Giarrusso-Fisher method[11] ( one function for one component )
- Walter Hannah method
I use functions by Robert Munafo.
(%i3) b3:c^3+2*c^2+(1-P)*c+(P-1)^2=0$ (%i4) solve(b3,c); (%o4) [ c=(-(sqrt(3)*%i)/2-1/2)*(((P-1)*sqrt(27*P^2-22*P+23))/(6*sqrt(3))-(27*P^2-36*P+25)/54)^(1/3)+ (((sqrt(3)*%i)/2-1/2)*(3*P+1))/(9*(((P- 1)*sqrt(27*P^2-22*P+23))/(6*sqrt(3))-(27*P^2-36*P+25)/54)^(1/3))-2/3, c=((sqrt(3)*%i)/2-1/2)* (((P-1)*sqrt(27*P^2-22*P+23))/(6*sqrt(3))-(27*P^2-36*P+25)/54)^(1/3)+ ((-(sqrt(3)*%i)/2-1/2)*(3*P+1))/(9*(((P-1)*sqrt(27*P^2-22*P+23)) /(6*sqrt(3))- (27*P^2-36*P+25)/54)^(1/3))-2/3, c=(((P-1)*sqrt(27*P^2-22*P+23))/(6*sqrt(3))-(27*P^2-36*P+25)/54)^(1/3)+ (3*P+1)/(9*(((P-1)*sqrt(27*P^2-22*P+23))/(6*sqrt(3))-(27*P^2-36*P+25)/54)^(1/3))
For each internal angle 
- point on unit circle
,
- points :
Result is a list of boundary points 
period 4
Boundary equation 
It is 1 equation with 2 variables. To solve it one has to compute 


For each internal angle 
- point on unit circle
,
- Boundary polynomial
- solve boundary equation
with respect to
. Result is 6 roots ( each for one of 6 period 4 components).
Result is a list of boundary points 
b4(w):=c^6 + 3*c^5 + (w/16+3)* c^4 + (w/16+3)* c^3 - (w/16+2)* (w/16-1)* c^2 - (w/16-1)^3;
l(t):=%e^(%i*t*2*%pi);
iMax:200; /* number of point */
dt:1/iMax;
/* point to point method of drawing */
t:0; /* angle in turns */
w:rectform(ev(l(t), numer)); /* "exponential form prevents allroots from working", code by Robert P. Munafo */
/* compute equation for given w */
per4:expand(b4(w));
/* compute 6 complex roots and save them to the list cc4 */
cc4:allroots(per4);
/* create new lists and save coordinates to draw it later */
xx4:makelist (realpart(rhs(cc4[1])), i, 1, 1);
yy4:makelist (imagpart(rhs(cc4[1])), i, 1, 1);
for j:2 thru 6 step 1 do
block
(
xx4:cons(realpart(rhs(cc4[j])),xx4),
yy4:cons(imagpart(rhs(cc4[j])),yy4)
);
for i:2 thru iMax step 1 do
block
( t:t+dt,
w:rectform(ev(l(t), numer)), /* code by Robert P. Munafo */
per4:expand(m4(w)),
cc4:allroots(per4),
for j:1 thru 6 step 1 do
block
(
xx4:cons(realpart(rhs(cc4[j])),xx4),
yy4:cons(imagpart(rhs(cc4[j])),yy4)
)
);
period 5
one computes in the same way as for period 4, only implicit function is different and there are 15 components.
period 6
one computes in the same way as for period 4, only implicit function is different (see Stephenson paper II ) and there are 27 components.
period 7
one computes in the same way as for period 4, only implicit function is different (degree in c is 63; see Stephenson paper III ) and there are 63 components.
period 8
Implicit equation 
Higher periods
"Although extension of the arithmethic method to higher orders is possible in principle, the computations become too big in space and time" (Stephenson paper III )
Relations between boundary equation, multiplier map, inverse multiplier map and multiplier
period 
|

|

|

|

|
|---|---|---|---|---|
| 1 | 
|

|

|

|
| 2 | 
|

|

|

|
| 3 | 
|

|
Symbolic solution of boundary equation is possible only for periods 1-3 ( with respect to 

Period 1
Solving with respect to 
Period 2
Solving is simple because these are degree 1 equations ( with respect to both 

Period 3
Solving with respect to 
Solving with respect to 
Maxima source code
/* batch file for Maxima http://maxima.sourceforge.net/ wxMaxima 0.7.6 http://wxmaxima.sourceforge.net archive copy at the Wayback Machine Maxima 5.16.1 http://maxima.sourceforge.net Using Lisp GNU Common Lisp (GCL) GCL 2.6.8 (aka GCL) Distributed under the GNU Public License. based on : http://www.mrob.com/pub/muency/brownmethod.html */ start:elapsed_run_time (); iMax:200; /* number of points to draw */ dt:1/iMax; /* unit circle D={w:abs(w)=1 } where w=l(t) t is angle in turns ; 1 turn = 360 degree = 2*Pi radians */ l(t):=%e^(%i*t*2*%pi); /* conformal maps from unit circle to hyperbolic component of Mandelbrot set of period 1-4 These functions ( maps ) are computed in other batch file */ /* --------------- inverse function of multiplier map : explicit function : c=gamma_p(P) where P = w/(2^period) ---------------- */ gamma1(P):=P-P^2; gamma2(P):=P - 1; gamma3a(P):=(-(sqrt(3)*%i)/2-1/2)*(((P-1)*sqrt(27*P^2-22*P+23))/(6*sqrt(3))-(27*P^2-36*P+25)/54)^(1/3)+ (((sqrt(3)*%i)/2-1/2)*(3*P+1))/(9*(((P-1)*sqrt(27*P^2-22*P+23))/(6*sqrt(3))-(27*P^2-36*P+25)/54)^(1/3))-2/3; gamma3b(P):=((sqrt(3)*%i)/2-1/2)*(((P-1)*sqrt(27*P^2-22*P+23))/(6*sqrt(3))-(27*P^2-36*P+25)/54)^(1/3)+ ((-(sqrt(3)*%i)/2-1/2)*(3*P+1))/(9*(((P- 1)*sqrt(27*P^2-22*P+23))/(6*sqrt(3))-(27*P^2-36*P+25)/54)^(1/3))-2/3; gamma3c(P):=(((P-1)*sqrt(27*P^2-22*P+23))/(6*sqrt(3))-(27*P^2-36*P+25)/54)^(1/3)+(3*P+1)/(9*(((P-1)*sqrt(27*P^2-22*P+23))/(6*sqrt(3))- (27*P^2-36*P+25) /54)^(1/3))-2/3; /* ---------- boundary equation (implicit function) b_p(P,c)=0 ------------------------------------------------------------------ */ b4(P):=c^6 + 3*c^5 + (P+3)* c^4 + (P+3)* c^3 - (P+2)*(P-1)*c^2 - (P-1)^3; /* ------ period 5 ------------- */ b5(P):=c^15 + 8*c^14 + 28*c^13 + (P + 60)*c^12 + (7*P + 94)*c^11 + (3*(P)^2 + 20*P + 116)*c^10 + (11*P^2 + 33*P + 114)*c^9 + (6*P^2 + 40*P + 94)*c^8 + (2*P^3 - 20*P^2 + 37*P + 69)*c^7 + (3*P - 11)*(3*P^2 - 3*P - 4)*c^6 + (P - 1)*(3*P^3 + 20*P^2 - 33*P - 26)*c^5 + (3*P^2 + 27*P + 14)*((P - 1)^2)*c^4 - (6*P + 5)*((P - 1)^3 )*c^3 + (P + 2)*((P - 1)^4)*c^2 - c*(P - 1)^5 + (P - 1)^6 ; /*-----period 6 ----------------------- */ b6(P):= c^27+ 13*c^26+ 78*c^25+ (293 - P)*c^24+ (792 - 10*P)*c^23+ (1672 - 41*P)*c^22+ (2892 - 84*P - 4*P^2)*c^21+ (4219 - 60*P - 30*P^2)*c^20+ (5313 + 155*P - 80*P^2)*c^19+ (5892 + 642*P - 57*P^2 + 4*P^3)*c^18+ (5843 + 1347*P + 195*P^2 + 22*P^3)*c^17+ (5258 + 2036*P + 734*P^2 + 22*P^3)*c^16+ (4346 + 2455*P + 1441*P^2 - 112*P^3 + 6*P^4)*c^15 + (3310 + 2522*P + 1941*P^2 - 441*P^3 + 20*P^4)*c^14 + (2331 + 2272*P + 1881*P^2 - 853*P^3 - 15*P^4)*c^13 + (1525 + 1842*P + 1344*P^2 - 1157*P^3 - 124*P^4 - 6*P^5)*c^12 + (927 + 1385*P + 570*P^2 - 1143*P^3 - 189*P^4 - 14*P^5)*c^11 + (536 + 923*P - 126*P^2 - 774*P^3 - 186*P^4 + 11*P^5)*c^10 + (298 + 834*P + 367*P^2 + 45*P^3 - 4*P^4 + 4*P^5)*(1-P)*c^9 + (155 + 445*P - 148*P^2 - 109*P^3 + 103*P^4 + 2*P^5)*(1-P)*c^8 + 2*(38 + 142*P - 37*P^2 - 62*P^3 + 17*P^4)*(1-P)^2*c^7 + (35 + 166*P + 18*P^2 - 75*P^3 - 4*P^4)*((1-P)^3)*c^6 + (17 + 94*P + 62*P^2 + 2*P^3)*((1-P)^4)*c^5 + (7 + 34*P + 8*P^2)*((1-P)^5)*c^4 + (3 + 10*P + P^2)*((1-P)^6)*c^3 + (1 + P)*((1-P)^7)*c^2 + -c*((1-P)^8) + (1-P)^9; /*-----------------------------------*/ /* point to point method of drawing */ t:0; /* angle in turns */ /* compute first point of curve, create list and save point to this list */ /* point of unit circle w:l(t); */ w:rectform(ev(l(t), numer)); /* "exponential form prevents allroots from working", code by Robert P. Munafo */ /* ---- period 1 -------------------*/ P:w/2; c1:gamma1(P); xx1:makelist (realpart(c1), i, 1, 1); /* save coordinates to draw it later */ yy1:makelist (imagpart(c1), i, 1, 1); /* -----period 2 --------------*/ P:P/2; c2:gamma2(P); xx2:makelist (realpart(c2), i, 1, 1); yy2:makelist (imagpart(c2), i, 1, 1); /* period 3 components */ P:P/2; c3:gamma3a(P); xx3a:makelist (realpart(c3), i, 1, 1); yy3a:makelist (imagpart(c3), i, 1, 1); c3:gamma3b(w); xx3b:makelist (realpart(c3), i, 1, 1); yy3b:makelist (imagpart(c3), i, 1, 1); c3:gamma3c(w); xx3c:makelist (realpart(c3), i, 1, 1); yy3c:makelist (imagpart(c3), i, 1, 1); /* period 4 */ P:P/2; per4:expand(b4(P)); /* compute equation for given w ( t) */ cc4:allroots(per4); /* compute 6 complex roots and save them to the list cc4 */ /* create new lists and save coordinates to draw it later */ xx4:makelist (realpart(rhs(cc4[1])), i, 1, 1); yy4:makelist (imagpart(rhs(cc4[1])), i, 1, 1); for j:2 thru 6 step 1 do block ( xx4:cons(realpart(rhs(cc4[j])),xx4), yy4:cons(imagpart(rhs(cc4[j])),yy4) ); /* period 5 */ P:P/2; per5:expand(b5(P)); /* compute equation for given w ( t) */ cc5:allroots(per5); /* compute 15 complex roots and save them to the list cc5 */ /* create new lists and save coordinates to draw it later */ xx5:makelist (realpart(rhs(cc5[1])), i, 1, 1); yy5:makelist (imagpart(rhs(cc5[1])), i, 1, 1); for j:2 thru 15 step 1 do block ( xx5:cons(realpart(rhs(cc5[j])),xx5), yy5:cons(imagpart(rhs(cc5[j])),yy5) ); /* period 6 */ P:P/2; per6:expand(b6(P)); /* compute equation for given w ( t) */ cc6:allroots(per6); /* compute 15 complex roots and save them to the list cc5 */ /* create new lists and save coordinates to draw it later */ xx6:makelist (realpart(rhs(cc6[1])), i, 1, 1); yy6:makelist (imagpart(rhs(cc6[1])), i, 1, 1); for j:2 thru 27 step 1 do block ( xx6:cons(realpart(rhs(cc6[j])),xx6), yy6:cons(imagpart(rhs(cc6[j])),yy6) ); /* ------------*/ for i:2 thru iMax step 1 do block ( t:t+dt, w:rectform(ev(l(t), numer)), /* "exponential form prevents allroots from working", code by Robert P. Munafo */ P:w/2, c1:gamma1(P), /* save values to draw it later */ xx1:cons(realpart(c1),xx1), yy1:cons(imagpart(c1),yy1), P:P/2, c2:gamma2(P), xx2:cons(realpart(c2),xx2), yy2:cons(imagpart(c2),yy2), P:P/2, c3:gamma3a(P), xx3a:cons(realpart(c3),xx3a), yy3a:cons(imagpart(c3),yy3a), c3:gamma3b(P), xx3b:cons(realpart(c3),xx3b), yy3b:cons(imagpart(c3),yy3b), c3:gamma3c(P), xx3c:cons(realpart(c3),xx3c), yy3c:cons(imagpart(c3),yy3c), /* period 4 */ P:P/2, per4:expand(b4(P)), cc4:allroots(per4), for j:1 thru 6 step 1 do block ( xx4:cons(realpart(rhs(cc4[j])),xx4), yy4:cons(imagpart(rhs(cc4[j])),yy4) ), /* period 5 */ P:P/2, per5:expand(b5(P)), /* compute equation for given w ( t) */ cc5:allroots(per5), /* compute 15 complex roots and save them to the list cc5 */ for j:1 thru 15 step 1 do block ( xx5:cons(realpart(rhs(cc5[j])),xx5), yy5:cons(imagpart(rhs(cc5[j])),yy5) ), /* period 6 */ P:P/2, per6:expand(b6(P)), /* compute equation for given w ( t) */ cc6:allroots(per6), /* compute 27 complex roots and save them to the list cc6 */ for j:1 thru 27 step 1 do block ( xx6:cons(realpart(rhs(cc6[j])),xx6), yy6:cons(imagpart(rhs(cc6[j])),yy6) ) ); stop:elapsed_run_time (); time:fix(stop-start); load(draw); draw2d( user_preamble="set terminal svg size 1000,1000;set out 'mysvg2.svg';set size square;set key out vert;set key bot center", pic_width = 1000, pic_height = 1000, yrange = [-1.5,1.5], xrange = [-2,1], title= concat("Boundaries of 53 hyperbolic components of Mandelbrot set made in ",string(time),"sec"), xlabel = "c.re ", ylabel = "c.im", point_type = dot, point_size = 5, points_joined =true, key = "one period 1 component = {c:c=(2*w-w*w)/4} ", color = red, points(xx1,yy1), key = "one period 2 component = {c:c=(w/4 -1)} ", color = green, points(xx2,yy2), key = "", color = red, points_joined =false, /* there are 3 curves so we can't join points */ points(xx3a,yy3a), points(xx3b,yy3b), key = "three period 3 components (blue)", points(xx3c,yy3c), key = "six period 4 components (magenta)", color = red, points(xx4,yy4), key = "fifteen period 5 components (black)", color = red, points(xx5,yy5), key = "27 period 6 components (black)", color = red, points(xx6,yy6) );
References
- ↑ Mario Rodriguez proposition in discussion about discrete dynamical system on the Maxima mailing list
- ↑ Multipliers of periodic orbits of quadratic polynomials and the parameter plane by Genadi Levin
- ↑ Algebraic solution of Mandelbrot orbital boundaries by Donald D. Cross
- ↑ A. Brown, Equations for Periodic Solutions of a Logistic Difference Equation, J. Austral. Math. Soc (Series B) 23, 78–94 (1981).
- ↑ John Stephenson : "Formulae for cycles in the Mandelbrot set", Physica A 177, 416-420 (1991); "Formulae for cycles in the Mandelbrot set II", Physica A 190, 104-116 (1992); "Formulae for cycles in the Mandelbrot set III", Physica A 190, 117-129 (1992)
- ↑ Wolf Jung : "Some Explicit Formulas for the Iteration of Rational Functions" , unpublished manuscript of August 1997 containing Maple code
- ↑ Thayer Watkins : The Structure of the Mandelbrot Set
- ↑ Enumeration of Features by Robert P. Munafo
- ↑ M. Lutzky: Counting hyperbolic components of the Mandelbrot set. Physics Letters A Volume 177, Issues 4-5, 21 June 1993, Pages 338-340
- ↑ Brown Method by Robert P. Munafo
- ↑ A Parameterization of the Period 3 Hyperbolic Components of the Mandelbrot Set Dante Giarrusso; Yuval Fisher Proceedings of the American Mathematical Society, Vol. 123, No. 12. (Dec., 1995), pp. 3731-3737
- ↑ Exact Coordinates by Robert P. Munafo
Acknowledgements
This program is not only my work but was done with help of many great people (see references). Warm thanks (:-))
مۆڵەتنامە
- تۆ ئازادی:
- بۆ بڵاکردنەوە – بۆ کۆپی کردن، دابەشکردن و دەستبەدەست ناردنی
- بۆ تێکەڵکردنەوە – بۆ سازاندنی کارەکە
- بەم مەرجانەی خوارەوە:
- دانەپاڵ – پێویستە باوەڕی گونجاو بدەیت، بەستەرێک بۆ مۆڵەتەکە دابین بکەیت و ئاماژە بەوە بکەیت کە ئایا گۆڕانکاری کراوە یان نا. دەتوانیت بە هەر شێوەیەکی گونجاو ئەوە بکەیت، بەڵام بە شێوەیەک نا کە وا دەربکەوێت کە مۆڵەتدەر پشتگیری تۆ یان بەکارهێنانەکەت بکات.
- بڵاوکردنەوەی گونجاو – ئەگەر لەسەر بنەمای ئەم کارە تێکەڵ، گۆڕان، یان ساز بکەی، پێویستە بەشدارییەکانت بە هەمان مۆڵەت یان هاوشێوەی مۆڵەتی ئەسڵی دابەش بکەی.
لێدوانەکان
بەندەکانی لەم پەڕگەیەدا دەردەکەون
depicts ئینگلیزی
some value
copyrighted ئینگلیزی
٤ ئازاری 2009
مێژووی پەڕگە
کرتە بکە لەسەر یەکێک لە ڕێکەوت/کاتەکان بۆ بینینی پەڕگەکە بەو شێوەی لەو کاتەدا بووە.
| ڕێکەوت/کات | ھێما | ئەندازە | بەکارھێنەر | تێبینی | |
|---|---|---|---|---|---|
| هەنووکە | ٠٣:٥٨، ٤ی ئازاری ٢٠٠٩ | 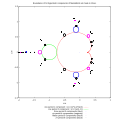 | ١٬٠٠٠ لە ١٬٠٠٠ (٨٥٣ کیلۆبایت) | Gringer | {{Information |Description={{en|1=SVG version of File:Components1.jpg, created using maxima by modifying preamble line of code to the following: user_preamble="set terminal svg size 1000,1000;set out 'mysvg.svg';set size square;set key out vert;set |
بەکارھێنانی پەڕگە
ئەم پەڕەیە ئەم پەڕگەیە بەکار دەھێنێت:
بەکارھێنانی سەرانسەریی پەڕگە
ئەم ویکیانەی دیکەی خوارەوەش ئەم پەڕگە بەکاردێنن:
- بەکارھێنان لە ar.wikipedia.org
- بەکارھێنان لە ca.wikipedia.org
- بەکارھێنان لە en.wikipedia.org
- بەکارھێنان لە en.wikibooks.org
- بەکارھێنان لە fi.wikipedia.org
- بەکارھێنان لە id.wikipedia.org
- بەکارھێنان لە ja.wikipedia.org
- بەکارھێنان لە pl.wikipedia.org
- بەکارھێنان لە ro.wikipedia.org
دراوی مێتا
ئەم پەڕگە زانیاری زێدەی ھەیە، کە لەوە دەچێت کامێرا یان ھێماگر (scanner) خستبێتیە سەری. ئەگەر پەڕگەکە لە حاڵەتی سەرەتاییەکەیەوە دەستکاری کرابێ، شایەد بڕێ لە بڕگەکان بە تەواوی زانیارەکانی وێنە گۆڕدراوەکە نیشان نەدەن.
| ناونیشانی وێنە | Produced by GNUPLOT 4.2 patchlevel 4 |
|---|













